Epidemic outbreaks, such as Ebola and the coronavirus disease (COVID-19), have underscored the critical role of mathematical modeling in understanding disease spread and informing public health interventions. By using mathematical models, epidemiologists and public health officials can predict the course of an outbreak, allocate resources effectively, and design intervention strategies. This article explores how mathematical models are used in epidemic analysis, focusing on the Ebola outbreak and the COVID-19 pandemic.
Understanding Epidemic Models
Mathematical models in epidemiology are tools that represent how diseases spread among populations. These models allow researchers to simulate different scenarios and predict the impact of various interventions, such as quarantine, vaccination, or social distancing. The primary goal of these models is to help health officials understand and control the dynamics of an epidemic.
Two of the most widely used classes of models are compartmental models and agent-based models. Compartmental models divide the population into distinct groups, or compartments, based on their disease status. The simplest example of a compartmental model is the Susceptible-Infected-Recovered (SIR) model. This model divides the population into three compartments:
Susceptible (S): People who are at risk of contracting the disease.
Infected (I): People who are currently infected and can transmit the disease.
Recovered (R): People who have recovered from the disease and are assumed to be immune.
In more complex models, compartments may also include Exposed (E) for individuals who have been infected but are not yet infectious, or Dead (D) for those who die from the disease. For Ebola and COVID-19, the extended versions of these models are often used to better capture the dynamics of these diseases.
Ebola Virus Disease (EVD)
Ebola is a deadly viral disease caused by the Ebola virus. It was first identified in 1976 and has since caused several outbreaks, the most severe of which occurred in West Africa between 2014 and 2016. The disease spreads through contact with bodily fluids of an infected person and has a high mortality rate, ranging from 25% to 90% depending on the strain and the quality of medical care.
Mathematical models for Ebola have played an essential role in understanding its spread. The early use of the SIR model was not sufficient because of the high mortality rate and the need to account for the latent period between infection and infectiousness. Instead, an SEIR (Susceptible-Exposed-Infected-Recovered) model was more suitable.
Susceptible (S): Individuals who are at risk of contracting Ebola.
Exposed (E): Individuals who have been infected but are not yet contagious.
Infected (I): Individuals who can transmit the virus to others.
Recovered (R): Individuals who have survived the infection and are assumed immune.
In the case of Ebola, mathematical models have been critical for understanding and predicting the course of outbreaks, including how long the epidemic might last and how the disease spreads in specific populations. Researchers have used models to identify "super-spreader" events—situations where one infected person could cause a disproportionate number of new infections—and assess the effectiveness of various interventions, such as quarantine and the distribution of vaccines.
Key Parameters in Ebola Modeling
Basic Reproduction Number (R₀): This is a measure of the contagiousness of a disease. It represents the average number of secondary cases generated from one infected individual in a fully susceptible population. For Ebola, R₀ typically ranges from 1.5 to 2.5.
Incubation Period: The time between exposure to the virus and the onset of symptoms. Ebola has an incubation period of 2 to 21 days, making it difficult to identify and isolate infected individuals early in the outbreak.
Case Fatality Rate (CFR): The proportion of individuals who die from the disease. Ebola has a high CFR, often ranging from 40% to 70%, making it a particularly deadly disease.
Effective Reproduction Number (Rₑ): Rₑ accounts for the impact of interventions (such as isolation and vaccination) on disease transmission. During the 2014-2016 outbreak, Rₑ dropped below 1 due to aggressive control measures, including contact tracing and isolation of affected individuals.
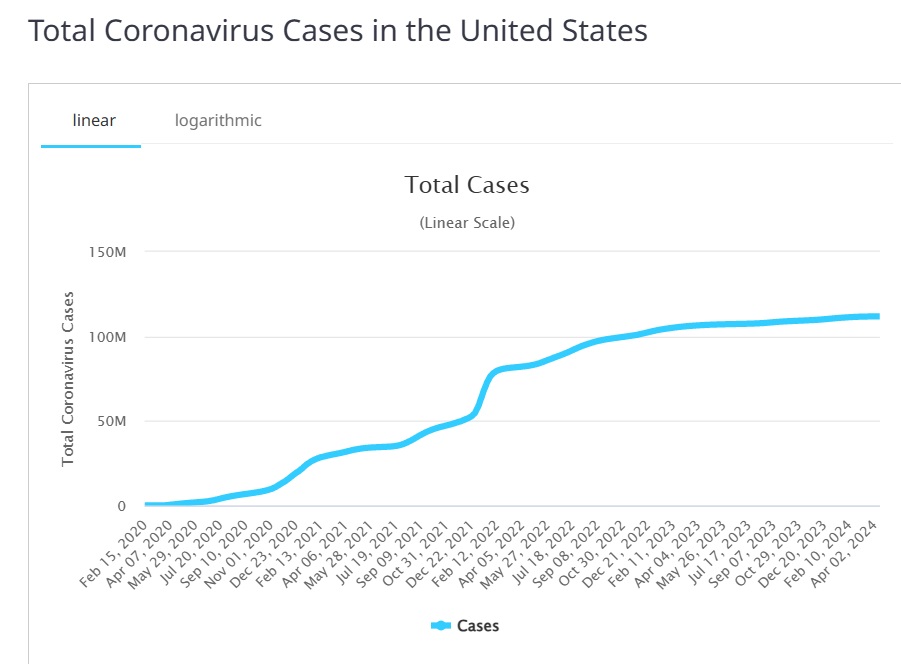
COVID-19 Pandemic
COVID-19, caused by the SARS-CoV-2 virus, emerged in December 2019 and rapidly spread across the globe, causing a pandemic. Unlike Ebola, which primarily spreads through direct contact with bodily fluids, COVID-19 is transmitted primarily through respiratory droplets, making it far more contagious. The COVID-19 pandemic has resulted in millions of infections and deaths worldwide, prompting an urgent need for effective modeling to understand and control its spread.
The mathematical models used in the analysis of COVID-19 are generally similar to those used for other infectious diseases, such as the SIR or SEIR models. However, COVID-19's transmissibility and the complexity of human behavior, coupled with the global nature of the pandemic, have made modeling more challenging.
Key Parameters in COVID-19 Modeling
Basic Reproduction Number (R₀): For COVID-19, R₀ has been estimated to range from 2.5 to 3.5, depending on the region and the specific variant. This suggests that each infected person can spread the virus to 2.5 to 3.5 other people on average.
Incubation Period: The incubation period for COVID-19 is typically 2 to 14 days, with most people showing symptoms within 4 to 5 days of exposure.
Asymptomatic and Pre-symptomatic Transmission: One of the most challenging aspects of COVID-19 is the ability of infected individuals to transmit the virus before they show symptoms. Asymptomatic carriers and pre-symptomatic individuals have played a critical role in the spread of the virus.
Case Fatality Rate (CFR): The CFR for COVID-19 varies by age and underlying health conditions. Globally, the CFR for COVID-19 has been estimated to be around 2% to 3%, though this figure is likely an underestimate due to underreporting and testing limitations.
Mathematical Modeling and Public Health Interventions
Mathematical models are used not only to understand the natural progression of epidemics but also to evaluate the impact of various public health interventions. During both the Ebola and COVID-19 outbreaks, models have been instrumental in informing decisions about quarantine, social distancing, testing, vaccination, and contact tracing.
1. Quarantine and Isolation
Quarantine and isolation measures aim to reduce the transmission of the disease by separating infected individuals from susceptible individuals. Models have been used to simulate the effects of quarantine on disease spread. For instance, during the Ebola outbreak in West Africa, models showed that early isolation of symptomatic individuals could significantly reduce the number of secondary cases.
Similarly, in the COVID-19 pandemic, the widespread use of quarantine and isolation (especially in the early stages of the outbreak) has been shown to reduce transmission, particularly in high-risk areas. The effectiveness of quarantine is highly dependent on compliance, the speed of implementation, and the duration of the isolation.
2. Vaccination
Vaccination plays a crucial role in controlling epidemics. For Ebola, an effective vaccine was developed during the 2014-2016 outbreak, and mathematical models helped predict its impact on disease transmission. In the case of COVID-19, the rapid development of vaccines was a major milestone. Mathematical models have been used to forecast the impact of vaccination campaigns and to determine the necessary vaccination coverage to achieve herd immunity.
3. Social Distancing and Public Health Campaigns
During the COVID-19 pandemic, the importance of social distancing, mask-wearing, and public health messaging has been underscored. Models showed that even modest reductions in contact rates could substantially decrease the spread of the virus, particularly in the absence of vaccines.
In contrast, during the Ebola outbreak, social distancing measures were less emphasized, as the primary mode of transmission was direct contact with bodily fluids. Instead, public health campaigns focused on educating people about the importance of avoiding contact with infected individuals, as well as safe burial practices.
Conclusion
Mathematical modeling plays a pivotal role in understanding and managing epidemics, from predicting the spread of the disease to evaluating the effectiveness of interventions. For diseases like Ebola and COVID-19, mathematical models provide critical insights that help guide public health responses. While both diseases present unique challenges, mathematical analysis has been instrumental in curbing their spread and saving lives. The continued development and refinement of these models will be crucial in managing future outbreaks and preventing pandemics.
In summary, the use of mathematical models in epidemic analysis is not just a theoretical exercise but a vital tool in public health decision-making. As the world faces an increasing number of infectious disease threats, mathematical models will continue to be at the forefront of efforts to predict, control, and ultimately eliminate the threat of pandemics.
You can learn these concepts and more at Dr Hock's maths and physics tuition.